티스토리 뷰
어쩌다 보니 올리게 되었다.
1번 문제

요약하면 최대값, 최소값이 변경되는 경우의 개수를 구하는 문제이다.
최소값, 최대값 변수를 초기에 설정하고 입력받은 값을 보면서 조건에 해당될때마다 더해서 값을 구해주면 된다.
시간 복잡도는 O(n)
import math
n=int(input())
l=list(map(int,input().split()))
inf=math.inf
mx=-inf
mn=inf
cnt=0
for i in range(n):
if mx<l[i]:
if mx!=-inf:
cnt+=1
mx=l[i]
if mn>l[i]:
if mn!=inf:
cnt+=1
mn=l[i]
print(cnt)2번 문제
2번 문제는 문제 사진은 없지만 요약하면 한점에서 다른 점으로 이동하는데 상하좌우, 대각선으로 한번에 1씩 갈 수 있다. 이때 걸리는 최소 거리를 구하는 문제인데, 이를 봤을 때 처음에는 bfs 문제라고 볼 수도 있다.
하지만 값의 범위가 매우 크기 때문에 그렇게 한다면 시간초과가 나게 된다.
이를 해결하는 방법은 생각보다 간단한데 두점간의 x 값의 차, y 값의 차를 비교해서 더 큰값을 출력하면 된다.
그 이유는 여기서 말하는 대각선은 수학으로 치면 기울기가 1 또는 -1, 즉 x 의 이동거리와 y의 이동거리가 같은 이동이다. 그러므로 x 또는 y 값이 같도록 움직인 뒤 한 방향으로 움직이면 그게 최소 거리가 되서 두점간의 x 값의 차, y 값의 차를 비교해서 더 큰값을 출력하면 된다.
시간복잡도 O(1)
import sys,math
from collections import deque
inf=math.inf
sys.setrecursionlimit(10**9)
input=sys.stdin.readline
a,b=map(int,input().split())
c,d=map(int,input().split())
case=abs(a-c)+abs(b-d)
ans=0
print(min(max(abs(d-b),abs(c-a)),case))
3번 문제

이 문제는 표에 나타나있는 그대로 각 단계마다 개수를 한개씩 늘려서 추가하는데 이때 k 번째 값을 출력하는 방법이다.
이를 그냥 하나하나 반복해서 구할려고 하면 k 값이 최대 2*10^9 가 되기 때문에 불가능 하다.
하지만 여기서 k 값이 2*10^9 가 최대라는 것과, 수열의 규칙성을 잘생각해보면 이 문제를 풀 수 있다.
일단 규칙성에 대해 알아보면 처음에는 수열의 원소 개수가 1, 두번째는 3, 3번째는 6, ... 계속 증가하는데 이때 값이 n단계일 때, n*(n+1)/2 개의 수열 원소를 가진 다는 것을 알수 있는데 이는 자명한 사실이니 증명을 하지는 않겠다.
다음은 k 값에 대한 것인데, k값이 2*10^9 보다 같거나 작다는 건, n*(n+1)/2 값이 k 보다 작은 값이 되야된다는 뜻이고 이를 이용해 n 의 최대값을 구해보면 10만이 아닌 6만 3천정도에서 끊긴다는 것을 알 수 있다.
이를 이용해 1부터 n의 최대 값까지 반복을 하면서 수열의 원소 개수가 k 보다 많을 때, 그 전의 개수에서 필요한 개수만큼 넘겨서 값을 출력해주면 된다. 이는 간단하게 반복문을 이용하거나 계산을 해주면 바로 구할 수 있다.
시간복잡도는 O(n) 이다.
import sys,math
from collections import deque
#n이 63246 부터 k 가 2*10**9 로 잡힘
inf=math.inf
sys.setrecursionlimit(10**9)
input=sys.stdin.readline
n,k=map(int,input().split())
l=list(map(int,input().split()))
for i in range(1,70001):
if i*(i+1)//2>=k:
R=(i-1)*i//2
for i in range(n):
R+=1
if R==k:
print(l[i])
sys.exit()
4번 문제
4번부터는 채점 사이트의 과부화? 로 모든 답이 출력초과로 떠 제대로 된 답을 확인할 수 없었고 그래서 이 풀이가 맞다고 확신할 수 없으니 참고만 바란다.
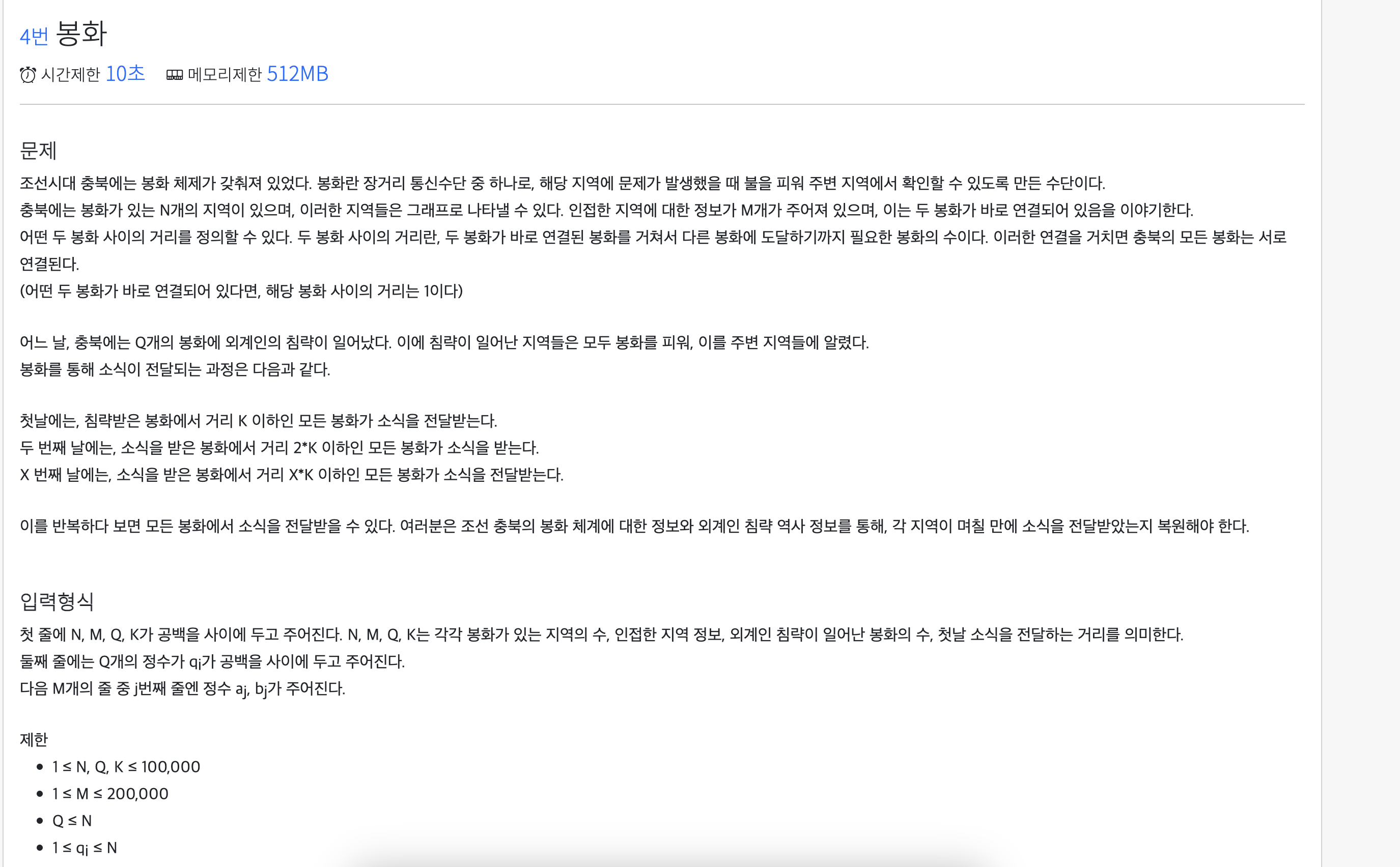
이문제를 요약하면 특정 점에서 시작하여 모든 점에 봉화가 켜지는 최소 시간을 구하는 문제이다.
이 문제는 두가지 풀이가 있는데 하나는 대회 때 생각한 풀이고 다른 하나는 대회가 끝난 후 생각한 풀이이다.
첫번째 풀이는 PriorityQueue 를 이용한 풀이다.
시작 노드를 pq(PriorityQueue)에 넣고 pq 에서 차례로 값을 가지고 와서 연결된 노드를 탐색하고, 탐색하면서 day 와 distance를 계산해 pq 에 넣어주는 방식을 사용하면 간단하게 문제를 풀 수 있다.
시간 복잡도는 O((V+E)log(Q)) 로 파이썬의 1초당 추정 최소 연산가능 횟수인 1000만을 기준으로 1억번의 계산안에 돌 수 있다.(하지만 입력코드만 넣어도 뜨는 출력초과때문에 제대로된 확인을 하지 못하였다.)
import sys,math
from collections import deque
from queue import PriorityQueue
input=sys.stdin.readline
n,m,q,k=map(int,input().split())
pq=PriorityQueue()
st=[-1]*(n+1)
cnt=0
for i in range(q):
a=int(input())
st[a]=0
cnt+=1
pq.put([1,0,a])
graph=[[]for i in range(n+1)]
for i in range(m):
a,b=map(int,input().split())
graph[a].append(b)
graph[b].append(a)
while cnt<n:
A=pq.get()
for i in range(len(graph[A[2]])):
if st[graph[A[2]][i]]==-1:
cnt+=1
st[graph[A[2]][i]]=A[0]
day=A[0]
distance=0
if A[1]+1>=A[0]*k:
day+=1
else:
distance=A[1]+1
pq.put([day,distance,graph[A[2]][i]])
for i in range(1,n):
print(st[i],end=" ")
print(st[n])
두번째 방법은 두 점 사이의 거리를 이용한 방법이다.
문제를 잘 생각해보면 결국 시작 점에서 가장 먼 점이 가장 늦게 봉화가 켜질 것이기 때문에 이를 이용해 모든 점간의 거리를 구해주면 된다.
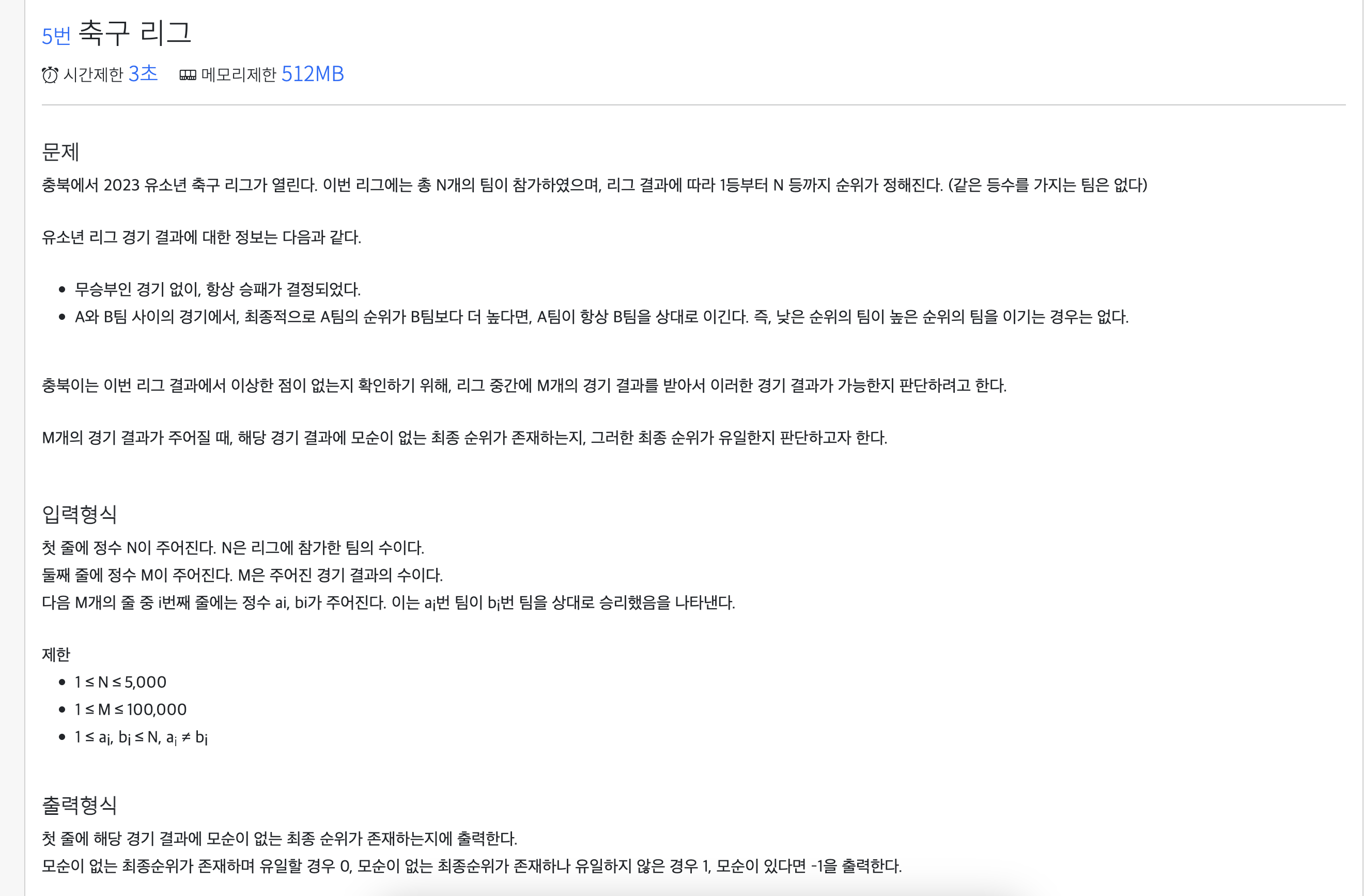
이 문제는 N개의 점을 차례로 나타낼 수 있는가를 묻는 문제이다. 그러므로 하나의 노드가 2개 이상의 자식을 가지거나, 2개 이상의 부모를 가지면 안 되고 물론 사이클도 생기면 안 된다. 이는 위상정렬의 방법을 사용하면 풀 수 있을 것이다.
'ps' 카테고리의 다른 글
| BOJ 23034(조별과제 멈춰!) 풀이 (0) | 2023.07.31 |
|---|---|
| BOJ 2493(탑) 풀이 (0) | 2023.07.31 |
| BOJ 15480(LCA와 쿼리)풀이 (0) | 2023.05.06 |
| BOJ 25402(트리와 쿼리)풀이 (0) | 2022.09.09 |
| BOJ 12722(Mousetrap (Large))풀이 (0) | 2022.08.04 |
- Total
- Today
- Yesterday
- 트리에서의 다이나믹 프로그래밍
- 개발
- 트리
- Python
- 알고리즘
- 세그먼트 트리
- 그래프 탐색
- 이분매칭
- 깊이 우선 탐색
- 자료구조
- 느리게 갱신되는 세그먼트 트리
- 그래프 이론
- 구현
- 수학
- 최소 스패닝 트리
- 누적 합
- C++
- 완전 탐색
- BOJ
- A Dance of Fire and Ice
- 다이나믹 프로그래밍
- codeforces
- 정렬
- discord bot
- 잡봇
- 이분 탐색
- KOI
- 그리디 알고리즘
- 자료 구조
- 선분 교차 판정
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |

